ESTADISTICA: 2016

UNIDAD 1

NOCIONES BÁSICAS DE ESTADÍSTICA

La estadística generalmente es definida como la rama de las matemáticas que se ocupa de reunir, organizar y analizar datos numéricos y así mismo que ayuda a resolver problemas como el diseño de experimentos y la toma de decisiones. Por ende lo que se busca con este trabajo, es hacer que a nuestros conocimientos se arraiguen las definiciones básicas de lo que es la estadística.

Se pretende incursionar en los primeros pasos sobre el uso y manejos de datos numéricos: distinguir y clasificar las características en estudio, enseñarnos a organizar y tabular las medidas obtenidas mediante la construcción de tablas de frecuencia y por último los métodos para elaborar una imagen que sea capaz de mostrar gráficamente unos resultados.

HISTORIA

La estadística (la forma femenina del alemán Statistik, y este derivado del italiano statista 'hombre de Estado' es una ciencia formal y una herramienta que estudia usos y análisis provenientes de una muestra representativa de datos, busca explicar las correlaciones y dependencias de un fenómeno físico o natural, de ocurrencia en forma aleatoria o condicional.

Es transversal a una amplia variedad de disciplinas, desde la física hasta las ciencias sociales, desde las ciencias de la salud hasta el control de calidad

1. Estadística descriptiva: Se dedica a la descripción, visualización y resumen de datos originados a partir de los fenómenos de estudio. Los datos pueden ser resumidos numérica o gráficamente. Ejemplos básicos de parámetros estadísticos son: la media y la desviación estándar. Algunos ejemplos gráficos son: histograma, pirámide poblacional, gráfico circular, entre otros.

1. Estadística inferencial: Se dedica a la generación de los modelos, inferencias y predicciones asociadas a los fenómenos en cuestión teniendo en cuenta la aleatoriedad de las observaciones. Se usa para modelar patrones en los datos y extraer inferencias acerca de la población bajo estudio. Estas inferencias pueden tomar la forma de respuestas a preguntas sí/no (prueba de hipótesis), estimaciones de unas características numéricas (estimación), pronósticos de futuras observaciones, descripciones de asociación (correlación) o modelamiento de relaciones entre variables (análisis de regresión). Otras técnicas de modelamiento incluyen análisis de varianza, series de tiempo y minería de datos.

Términos Importantes

Población: grupo entero motivo de estudio

Muestra: Parte de la población que es representativa

Variables: Es una características que puede tener diferentes valores para los distintos elementos de la población

Clasificación de las Variables

Cualitativas: los datos se describen mediante palabras eje: sexo, estado civil

Cuantitativas: los datos se describen o registran mediante números eje: peso, estatura, numero de hijos.

Las Variables Cuantitativas pueden ser:

Discretas, Continuas.

División de la estadística

La Estadística para su mejor estudio se ha dividido en dos grandes ramas: la Estadística Descriptiva y la Inferencial.

• Estadística Descriptiva: consiste sobre todo en la presentación de datos en forma de tablas y gráficas. Esta comprende cualquier actividad relacionada con los datos y está diseñada para resumir o describir los mismos sin factores pertinentes adicionales; esto es, sin intentar inferir nada que vaya más allá de los datos, como tales.

• Estadística Inferencial: se deriva de muestras, de observaciones hechas sólo acerca de una parte de un conjunto numeroso de elementos y esto implica que su análisis requiere de generalizaciones que van más allá de los datos. Como consecuencia, la característica más importante del reciente crecimiento de la estadística ha sido un cambio en el énfasis de los métodos que describen a métodos que sirven para hacer generalizaciones. La Estadística Inferencial investiga o analiza una población partiendo de una muestra tomada.

6 FASES DE LA INVESTIGACIÓN ESTADÍSTICA

A: Planeacion y preparación

B: Fase de la recolección

C: Critica y codificación

D: Tabulacion o procesamiento

E: Análisis e interpretación

F: Publicación

MAPA MENTAL

UNIDAD 2

SUMATORIA Y PRODUCTORIAS

Sumatoria:

La sumatoria es un tema difícil de trabajar ya que con todos los elementos de una determinada sucesión.

Por lo cual para lograr facilitar este trabajo se conviene representar la adicion de los términos en forma abreviada mediante el signo ∑,el cual se acompaña de una formula o termino general que define a la sucesión y el rango de valores que se tomara en la variable correspondientes.

" Por lo que esta se entiende como la suma de un finito de números" denotados de la siguiente manera,

Donde la Notación:

se lee:

Suma de X sub-i (ó sigma sub-i) donde i asume todos los valores de 1 hasta n, ó simplemente suma de X sub-i donde i va de 1 a n.

Las sumatorias se pueden representar bajo dos tipos de notaciones:

* Notación suma abierta: Esta notación va de una representación de sumatoria a cada uno de los elementos que la componen, por ejemplo:

* Notación suma pertinente: Esta notación es al contrario de la suma abierta, va de la representación de cada uno de los elementos de una sumatoria a su representación matemática

Productorias

El productorio también conocido como multiplicatoria o simplemente producto (por denotarse como una letra pi mayúscula), es un notación matemática que representa una multiplicación de una cantidad arbitraria (finita o infinita).

LA NOTACIÓN:

La notación se expresa con la letra griega pi mayúscula Π de la siguiente manera:

\prod_{k=m}^n a_k = a_m \cdot a_{m+1} \cdot \quad \dots \quad \cdot a_{n}

Para todos los valores m < n, si m = n tenemos que:

m = n \; , \quad \prod_{k=m}^n a_k = \prod_{k=m}^m a_k = a_{m}

En el caso de que m sea mayor que n, m > n, se le asigna el valor del elemento neutro de la multiplicación, el uno:

m > n \; , \quad \prod_{k=m}^n a_k = 1

Se puede definir por inducción como sigue.

1. Se define

\prod_{k=1}^1 a_k = a_1

2. Supuesta definida para un n ≥ 1 fijo, se define

\prod_{k=1}^{n+1} a_k = \left ( \prod_{k=1}^n a_k \right ) a_{n+1}

EJEMPLO:

Se puede usar el productorio para definir otras igualdades importantes. Así, tomando n=1 y aplicando la segunda igualdad se obtiene:

\prod_{k=1}^2 a_k = \left( \prod_{k=1}^1 a_k \right) (a_2) = a_1 a_2

Definida para n=2, se puede aplicar otra vez la segunda igualdad con n=2 para luego obtener

\prod_{k=1}^3 a_k = \left( \prod_{k=1}^2 a_k \right) (a_3) = (a_1 a_2) a_3

Así, usando la propiedad asociativa de la multiplicación, el producto

\mathit{(a_1a_2)a_3} \,\!

es el mismo que

\mathit{a_1(a_2a_3)} \,\!

y, por lo tanto, podemos prescindir del uso de paréntesis sin peligro de confusión y usar simplemente

a_1 \, a_2 \, a_3 = \prod_{k=1}^3 a_k

Se puede entonces, usar este razonamiento para cualquier

n \in \mathbb{N}

sin que haya peligro de confusión.

Otro ejemplo de productorio muy conocido es el que se utiliza para definir n! (n factorial) como sigue:

\prod_{k=1}^n k = n!

Se define

0! = 1! = 1

MAPA MENTAL

UNIDAD 3

TABLAS DE FRECUENCIAS Y GRÁFICOS ESTADÍSTICOS

1: Tablas y gráficos estadísticos para variables cualitativas y cuantitativas discretas

Frecuencia absoluta= (ni) = Fi

La frecuencia absoluta de un dato, corresponde al numero de veces que se repite el dato.

Frecuencia Relativa= (Hi= Fr)

+La frecuencia relativa de un dato, es el cociente entre las frecuencias absoluta del dato y el numero total de datos. La frecuencia relativa se puede presentar de 3 formas: Fracción, decimal y porcentaje.

Cuando se realiza un estudio estadístico sobre una variable (por ejemplo, altura de los niños de una clase, equipo de fútbol preferido por los alumnos de un colegio, etc.) se comienza por obtener información (se mide a los niños, se les pregunta, etc.).

Dato estadístico es cada una de las informaciones que se obtiene (por ejemplo, Pedro mide 1,65 cm; Julián es aficionado del Barcelona, etc).

Vemos que el dato estadístico puede ser numérico (por ejemplo, estatura) o cualitativo (por ejemplo, equipo de fútbol preferido).

Los datos obtenidos en la observación hay que ordenarlos y recogerlos en una tabla que se denomina tabla estadística.

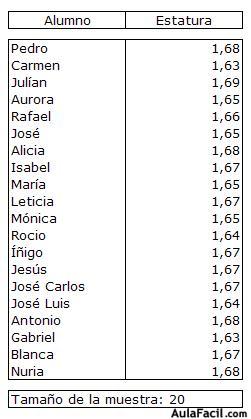El número de observaciones realizadas se denomina tamaño de la muestra.

La frecuencia absoluta de un dato es el número de veces que se da un resultado concreto y la frecuencia relativa es el porcentaje que representa la frecuencia absoluta respecto del total.

La media aritmética representa el valor medio que toman los datos de una observación estadística. Se calcula sumando todos los resultados y dividiendo la suma entre el número de registros. La media aritmética tan sólo se puede calcular con datos numéricos (no se puede calcular con datos cualitativos).

Moda: es el resultado más repetido en una observación estadística (se puede calcular con datos numéricos y cualitativos).

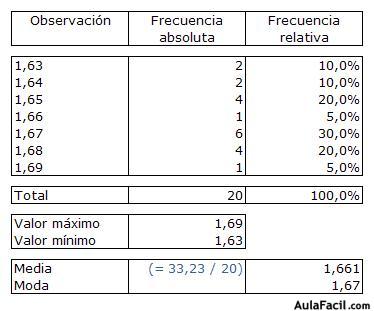La media la hemos calculado sumando las 20 estaturas (33,23 cm) y dividiéndolo entre el número de datos (20).

Las frecuencias absolutas o relativas se pueden representar sobre una gráfica de barras en la que la altura de cada barra representa el valor de la frecuencia.

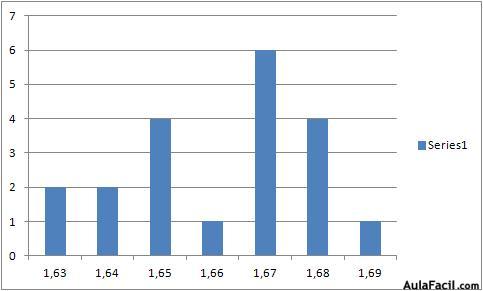En este gráfico hemos representado la frecuencia absoluta.

También se puede utilizar el diagrama de sectores para representar las frecuencias (absolutas o relativas). Se utiliza un círculo dividido en sectores; cada sector representa cada uno de los posibles valores que toma la variable que se mide; la superficie del sector mide el valor de la frecuencia (absoluta o relativa).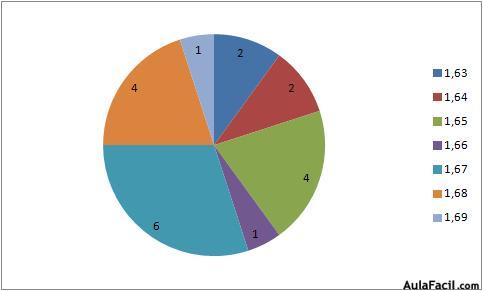

MAPA MENTAL

UNIDAD 4

MEDIDAS DE TENDENCIA CENTRAL O ESTADIGRAFOS DE POSICIÓN

Las medidas de tendencia central son valores numéricos que se utiliza para representar o describir un conjunto de datos. entonces las medidas de tendencia central mas utilizadas son:

La medida aritmética, la mediana, la moda, la media armónica, la media geométrica, los estadigrafos de posición que mas se utilizan son mediana,

Al describir grupos de diferentes observaciones, con frecuencia es conveniente resumir la información con un solo número. Este número que, para tal fin, suele situarse hacia el centro de la distribución de datos se denomina medida o parámetro de tendencia central o de centralización. Cuando se hace referencia únicamente a la posición de estos parámetros dentro de la distribución, independientemente de que ésta esté más o menos centrada, se habla de estas medidas como medidas de posición.¹ En este caso se incluyen también los cuantiles entre estas medidas

* La media aritmética: (X)

para calcular la media aritmética, se suman los valores de los datos y se divide dicha suma entre el numero total de datos.

La Media Aritmetica

La media aritmética (también llamada promedio o simplemente media) de un conjunto finito de números es el valor característico de una serie de datos cuantitativos objeto de estudio que parte del principio de la esperanza matemática o valor esperado, se obtiene a partir de la suma de todos sus valores dividida entre el número de sumandos. Cuando el conjunto es una muestra aleatoria recibe el nombre de media muestral siendo uno de los principales estadísticos maestrales.

Definición

Dados los n números

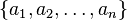\{a_1, a_2, \ldots, a_n\}

, la media aritmética se define como:

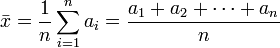$\bar{x} = \frac{1}{n} \sum_{i=1}^{n} a_i = \frac{a_1+a_2+\cdots+a_n}{n}$

Por ejemplo, la media aritmética de 8, 5 y -1 es igual a:

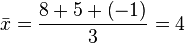$\bar{x} = \frac{ 8 + 5 + \left ( -1 \right ) }{3} = 4$

Se utiliza la letra X con una barra horizontal sobre el símbolo para representar la media de una muestra (

\overline{X}

), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.

En otras palabras, es la suma de n valores de la variable y luego dividido por n : donde n es el número de sumandos, o en el caso de estadística el número de datos se da el resultado.

DIAGRAMA DE BARRAS

Un diagrama de barras, también conocido como gráfico de barras o diagrama de columnas, es una forma de representar gráficamente un conjunto de datos o valores, y está conformado por barras rectangulares de longitudes proporcionales a los valores representados. Los gráficos de barras son usados para comparar dos o más valores. Las barras pueden orientarse verticalmente u horizontalmente.

EJEMPLO

Este diagrama de ejemplo está basado en los resultados de la Elección del Parlamento Europeo en el 2004 y en el de 1999. La tabla siguiente lista el número de asientos asignadas a cada partido. Los resultados de 1999 han sido multiplicados por 1.16933, para compensar el cambio en el número de asientos entre estos años.

Grupo	Asientos (2004)	Asientos (1999) a escala
EURO	33	33 33	33
EFA	33	33	33	EDD	33	33	33	ELDR	67	60
EPP	276	272
UEN	27	36
Otros	66	29

MAPA MENTAL

PASATIEMPO

GLOSARIO

Estadística: La estadística es una ciencia formal y una herramienta que estudia usos y análisis provenientes de una muestra representativa de datos, busca explicar las correlaciones y dependencias de un fenómeno físico o natural, de ocurrencia en forma aleatoria o condicional.

Diagrama: es un dibujo geométrico, muy utilizado en ciencia, en educación y en comunicación; con el que se obtiene la presentación gráfica de una proposición, de la resolución de un problema, de las relaciones entre las diferentes partes o elementos de un conjunto o sistema, o de la regularidad en la variación de un fenómeno que permite establecer algún tipo de ley

Tamaño: Las dimensiones o medidas de un objeto:Para objetos de una dimensión, es la longitud, altura o anchura.Para objetos de dos dimensiones, es la superficie.Para objetos de tres dimensiones, es el volumen.La altura o longitud o anchura de un ser vivo.La estatura de una persona.En informática, es la cantidad de bytes que ocupa un archivo o carpeta de cualquiera tipo, aunque esté vacío (tamaño cero).Hablando de ciudades, casi siempre se refiere su población, rara vez a su extensión o superficie.

Muestra: En estadística, una muestra es un subconjunto de casos o individuos de una población estadística. En diversas aplicaciones interesa que una muestra sea una muestra representativa y para ello debe escogerse una técnica de muestreo adecuada que produzca una muestra aleatoria adecuada (contrariamente se obtiene una muestra sesgada cuyo interés y utilidad es más limitado dependiendo del grado de sesgo que presente). La muestra es por lo tanto el grupo al que se le aplican las pruebas.

PRESENTADO POR:

YISEL ANDREA SANCHEZ FAJARDO
NESTOR CERQUERA
OSCAR VILLARREAL
(Administración de Empresas)

domingo, 15 de mayo de 2016